mirror of
https://github.com/jkriege2/JKQtPlotter.git
synced 2025-02-19 02:39:26 +08:00
78 lines
5.0 KiB
Markdown
78 lines
5.0 KiB
Markdown
# Example (JKQTPlotter): Plotting Parsed Mathematical Functions as Line Graphs {#JKQTPlotterParsedFunctionPlot}
|
|
|
|
# Plot Function f(x)
|
|
|
|
This project (see `./examples/parsedfunctionplot/`) demonstrates how to plot mathematical functions as line graphs. The functions are defined as strings that will be evaluated with the equation parser, integrated into JKQTPlotter.
|
|
|
|
Note: See the example [Plotting Mathematical Functions as Line Graphs](https://github.com/jkriege2/JKQtPlotter/tree/master/examples/functionplot) if you don't want to draw parsed functions, but want to provide a C function, or C++ functor!
|
|
|
|
Adding an evaluated funtion to a graph is very simple:
|
|
```.cpp
|
|
JKQTPXParsedFunctionLineGraph* parsedFunc=new JKQTPXParsedFunctionLineGraph(plot);
|
|
parsedFunc->setFunction("sin(x*8)*exp(-x/4)");
|
|
parsedFunc->setTitle("user function");
|
|
```
|
|
As you can see a graph of the type `JKQTPXParsedFunctionLineGraph` is used, which plots a function that depends on the variable `x`. The given function is parsed and evaluated (see [`lib/jkqtcommon/jkqtpmathparser.h`](https://github.com/jkriege2/JKQTPlotter/blob/master/lib/jkqtcommon/jkqtpmathparser.h) for details on the features of the math parser). An intelligent drawing algorithm chooses the number of control points for drawing a smooth graph, with sufficient amount of details, by evaluating locally the slope of the function.
|
|
|
|
In the example in [`examples/parsedfunctionplot/parsedfunctionplot.cpp`](https://github.com/jkriege2/JKQtPlotter/tree/master/examples/parsedfunctionplot/parsedfunctionplot.cpp) we do not simply set a fixed function, but add a `QLineEdit` which allows to edit the function and redraws it, once ENTER is pressed:
|
|
```.cpp
|
|
JKQTPlotter* plot=new JKQTPlotter(&mainWin);
|
|
QLineEdit* edit=new QLineEdit(&mainWin);
|
|
edit->setToolTip("enter a function in dependence of the variable <tt>x</tt> and press ENTER to update the graph");
|
|
|
|
// ...
|
|
|
|
|
|
// 2. now we add a JKQTPXParsedFunctionLineGraph object, which will draw the function from
|
|
// the line edit
|
|
JKQTPXParsedFunctionLineGraph* parsedFunc=new JKQTPXParsedFunctionLineGraph(plot);
|
|
plot->addGraph(parsedFunc);
|
|
// finally we connect the line edit with the graph, whenever RETURN is pressed,
|
|
// the graph is updated:
|
|
auto updateGraphFunctor=
|
|
[=]() {
|
|
parsedFunc->setTitle("user function: \\verb{"+edit->text()+"}");
|
|
parsedFunc->setFunction(edit->text());
|
|
plot->redrawPlot();
|
|
};
|
|
QObject::connect(edit, &QLineEdit::returnPressed, updateGraphFunctor);
|
|
QObject::connect(edit, &QLineEdit::editingFinished, updateGraphFunctor);
|
|
edit->setText("sin(x*8)*exp(-x/4)");
|
|
updateGraphFunctor();
|
|
```
|
|
|
|
|
|
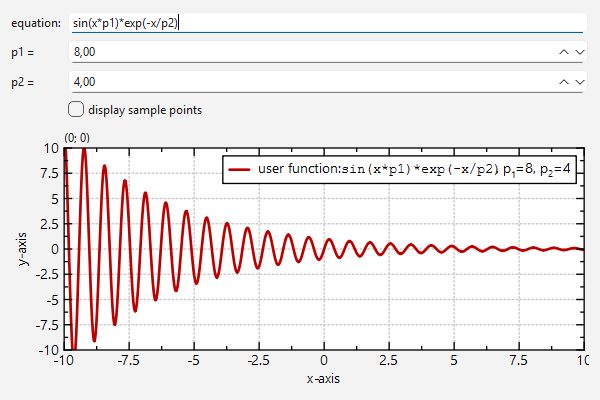
This code snippet results in a plot like this:
|
|
|
|
|
|
|
|
# Plotting with parameters
|
|
|
|
As shown in [Plotting Mathematical Functions as Line Graphs](https://github.com/jkriege2/JKQtPlotter/tree/master/examples/functionplot) you can also use externally set parameters in a plot function. These parameters can be double numbers and may be set with either as an internal parameter vector, or may be read from a parameter column (as shown in the [linked example](https://github.com/jkriege2/JKQtPlotter/tree/master/examples/functionplot)). These parameters are available as variables `p1`, `p2`, ... in the function string. Here is a small example:
|
|
|
|
```.cpp
|
|
JKQTPXParsedFunctionLineGraph* parsedFunc=new JKQTPXParsedFunctionLineGraph(plot);
|
|
parsedFunc->setFunction("sin(x*p1)*exp(-x/p2)");
|
|
parsedFunc->setParamV(/*p1=*/8, /*p2=*/4);
|
|
parsedFunc->setTitle("user function");
|
|
```
|
|
|
|
# Plot Function f(y)
|
|
|
|
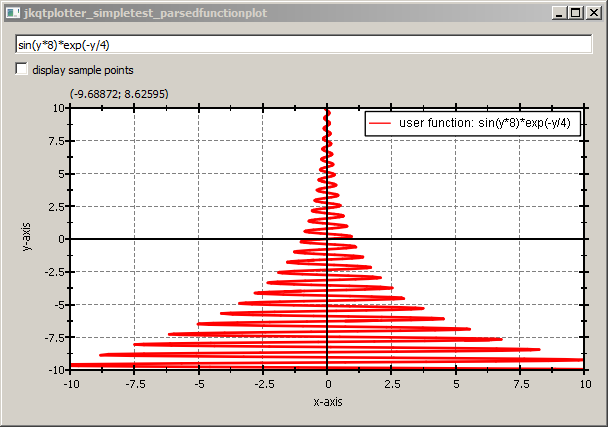
If you use the graph class `JKQTPYParsedFunctionLineGraph` instead of `JKQTPXParsedFunctionLineGraph`, you can plot functions `x=f(y)` (instead of `y=f(x)`). The function from the example above will then ahve to be changed to `sin(y*8)*exp(-y/4)` and the result will look like this:
|
|
|
|
|
|
|
|
|
|
# Properties of the Adaptive Plotting Algorithm
|
|
|
|
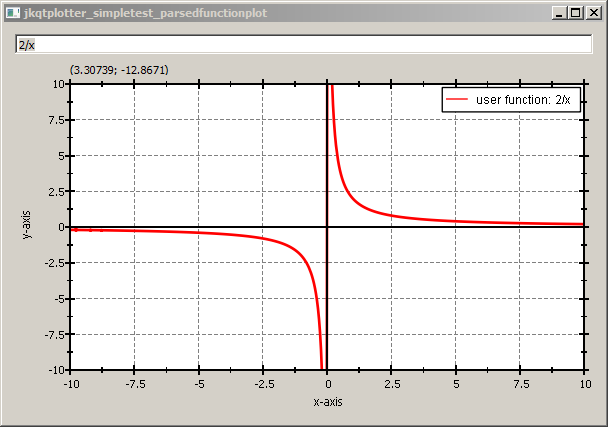
The adaptive capabilities of the rendering algorithm can be seen, when plotting e.g. `2/x`, which is drawn smoothely, even around the undefined value at `x=0`:
|
|
|
|
|
|
|
|
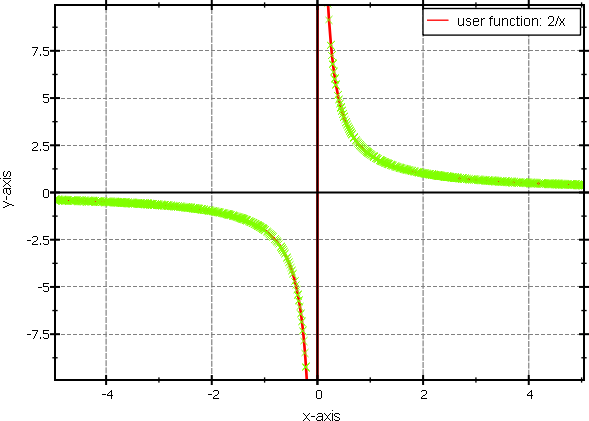
With an additional checkbox in this example, you can switch drawing the actual sample points of the drawing algorithm on and off, by calling `parsedFunc->setDisplaySamplePoints(...)`. This can be used to debug the drawing algorithm and explore its parameters (which you can set with `setMinSamples()`, `setMaxRefinementDegree()`, `setSlopeTolerance()`, `setMinPixelPerSample()`). Here is an example of a 2/x function with shown sample points:
|
|
|
|
|
|
|
|
|