|
|
||
|---|---|---|
| .. | ||
| CMakeLists.txt | ||
| datastore_regression_and_lib.pro | ||
| datastore_regression.cpp | ||
| datastore_regression.pro | ||
| README.md | ||
Tutorial (JKQTPDatastore): Regression Analysis (with the Statistics Library)
[JKQTPlotterBasicJKQTPDatastore]: @ref JKQTPlotterBasicJKQTPDatastore "Basic Usage of JKQTPDatastore" [JKQTPlotterBasicJKQTPDatastoreIterators]: @ref JKQTPlotterBasicJKQTPDatastoreIterators "Iterator-Based usage of JKQTPDatastore" [JKQTPlotterBasicJKQTPDatastoreStatistics]: @ref JKQTPlotterBasicJKQTPDatastoreStatistics "Advanced 1-Dimensional Statistics with JKQTPDatastore" [JKQTPlotterBasicJKQTPDatastoreRegression]: @ref JKQTPlotterBasicJKQTPDatastoreRegression "Regression Analysis (with the Statistics Library)" [JKQTPlotterBasicJKQTPDatastoreStatisticsGroupedStat]: @ref JKQTPlotterBasicJKQTPDatastoreStatisticsGroupedStat "1-Dimensional Group Statistics with JKQTPDatastore" [JKQTPlotterBasicJKQTPDatastoreStatistics2D]: @ref JKQTPlotterBasicJKQTPDatastoreStatistics2D "Advanced 2-Dimensional Statistics with JKQTPDatastore" [statisticslibrary]: @ref jkqtptools_math_statistics "JKQTPlotter Statistics Library"
This tutorial project (see ./examples/datastore_statistics/) explains several advanced functions of JKQTPDatastore in combination with the statisticslibrary conatined in JKQTPlotter.
Note that there are additional tutorial explaining other aspects of data mangement in JKQTPDatastore:
- [JKQTPlotterBasicJKQTPDatastore]
- [JKQTPlotterBasicJKQTPDatastoreIterators]
- [JKQTPlotterBasicJKQTPDatastoreStatistics]
- [JKQTPlotterBasicJKQTPDatastoreRegression]
- [JKQTPlotterBasicJKQTPDatastoreStatisticsGroupedStat]
- [JKQTPlotterBasicJKQTPDatastoreStatistics2D]
[TOC]
The source code of the main application can be found in datastore_regression.cpp.
This tutorial cites only parts of this code to demonstrate different ways of performing regression analysis.
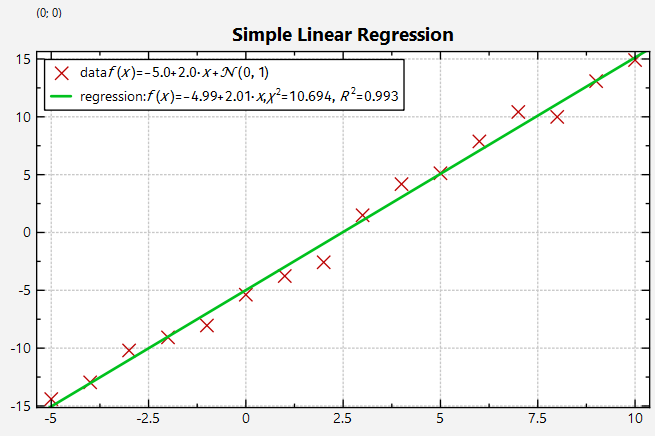
Simple Linear Regression
First we generate a set of datapoints (x,y), which scatter randomly around a linear function.
std::random_device rd; // random number generators:
std::mt19937 gen{rd()};
std::normal_distribution<> d1{0,1};
double a0=-5;
double b0=2;
size_t colLinX=datastore1->addColumn("lin data, x");
size_t colLinY=datastore1->addColumn("lin data, y");
for (double x=-5; x<=10; x++) {
datastore1->appendToColumn(colLinX, x);
datastore1->appendToColumn(colLinY, a0+b0*x+d1(gen));
}
... and we visualize this data with a simple scatter graph:
JKQTPXYLineGraph* graphD;
plot1->addGraph(graphD=new JKQTPXYLineGraph(plot1));
graphD->setXYColumns(colLinX, colLinY);
graphD->setDrawLine(false);
graphD->setTitle("data");
Now we can caluate the regression line (i.e. the two regression coefficients a and b of the function \c f(x)=a+b*x) using the function jkqtpstatLinearRegression() from the [statisticslibrary]:
double coeffA=0, coeffB=0;
jkqtpstatLinearRegression(datastore1->begin(colLinX), datastore1->end(colLinX), datastore1->begin(colLinY), datastore1->end(colLinY), coeffA, coeffB);
... and add a JKQTPXFunctionLineGraph to draw the resulting linear function:
JKQTPXFunctionLineGraph *graphRegLine=new JKQTPXFunctionLineGraph(plot1);
graphRegLine->setSpecialFunction(JKQTPXFunctionLineGraph::SpecialFunction::Line);
graphRegLine->setParamsV(coeffA, coeffB);
graphRegLine->setTitle(QString("regression: $f(x) = %1 + %2 \\cdot x$").arg(jkqtp_floattolatexqstr(coeffA)).arg(jkqtp_floattolatexqstr(coeffB)));
plot1->addGraph(graphRegLine);
These two steps can be simplified using an "adaptor":
jkqtpstatAddLinearRegression(plot1->getPlotter(), datastore1->begin(colLinX), datastore1->end(colLinX), datastore1->begin(colLinY), datastore1->end(colLinY));
... or even shorter:
jkqtpstatAddLinearRegression(graphD);
Here the x- and y-columns from the JKQTPXYGraph-based graph graphD (see above) are used as datasources for the plot.
The plot resulting from any of the variants above looks like this:
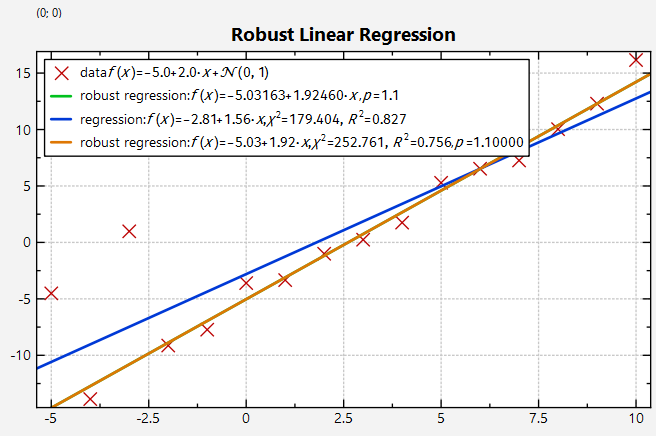
Robust Linear Regression
Sometimes data contains outliers that can render the results of a regression analysis inaccurate. For such cases the [statisticslibrary] offers the function jkqtpstatRobustIRLSLinearRegression(), which is a drop-in replacement for jkqtpstatLinearRegression() and solves the optimization problem a) in the Lp-norm (which is more robust to outliers) and b) uses the iteratively reweighted least-squares algorithm (IRLS), which performs a series of regressions, where in each instance the data-points are weighted differently. The method assigns a lower weight to those points that are far from the current best-fit (typically the outliers) and thus slowly comes nearer to an estimate that is not distorted by the outliers.
To demonstrate this method, we use the same dataset as above, but add a few outliers:
std::random_device rd; // random number generators:
std::mt19937 gen{rd()};
std::normal_distribution<> d1{0,1};
double a0=-5;
double b0=2;
size_t colLinX=datastore1->addColumn("lin data, x");
size_t colLinY=datastore1->addColumn("lin data, y");
for (double x=-5; x<=10; x++) {
datastore1->appendToColumn(colLinX, x);
if (jkqtp_approximatelyEqual(x, -5)||jkqtp_approximatelyEqual(x, -3)) datastore1->appendToColumn(colRLinY, a0+b0*x+d1(gen)+12);
else datastore1->appendToColumn(colRLinY, a0+b0*x+d1(gen));
}
Note the outliers ar x=-5 and x=-3!
With this dataset we can use the same code as above, but with jkqtpstatRobustIRLSLinearRegression() instead of jkqtpstatLinearRegression():
double coeffA=0, coeffB=0;
jkqtpstatRobustIRLSLinearRegression(datastore1->begin(colRLinX), datastore1->end(colRLinX), datastore1->begin(colRLinY), datastore1->end(colRLinY), coeffA, coeffB);
JKQTPXFunctionLineGraph *graphRegLine=new JKQTPXFunctionLineGraph(plot3);
graphRegLine->setSpecialFunction(JKQTPXFunctionLineGraph::SpecialFunction::Line);
graphRegLine->setParamsV(coeffA, coeffB);
graphRegLine->setTitle(QString("robust regression: $f(x) = %1 + %2 \\cdot x$").arg(jkqtp_floattolatexqstr(coeffA)).arg(jkqtp_floattolatexqstr(coeffB)));
plot3->addGraph(graphRegLine);
Also for the robust regression, there are two shortcuts in the form of "adaptors":
jkqtpstatAddRobustIRLSLinearRegression(plot3->getPlotter(), datastore1->begin(colRLinX), datastore1->end(colRLinX), datastore1->begin(colRLinY), datastore1->end(colRLinY));
and
jkqtpstatAddRobustIRLSLinearRegression(graphD);
The following screenshot shows the result of the IRLS regression analysis and for comparison the normal linear regression for the same dataset (plotted using jkqtpstatAddLinearRegression(graphD);):
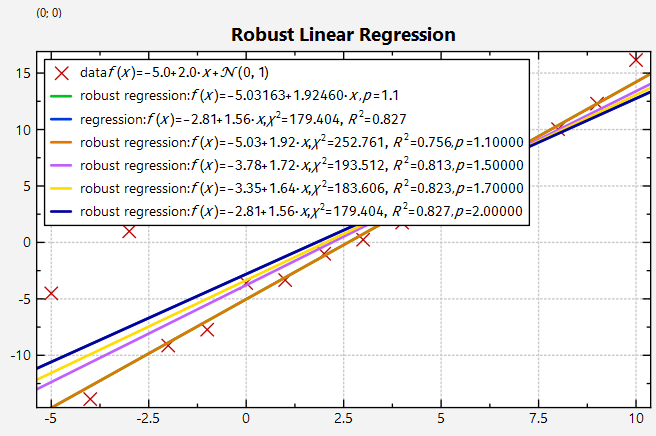
The following screenshot shows the influence of the regularization parameter p (default value 1.1) onto the fit result:
- the closer
pis to 1, the more robust the fit is (it is closer to the L1-norm) - the closer
pis to 2, the closer the fit is to the least squares solution (i.e. the normal regression obtained with the L2 norm)
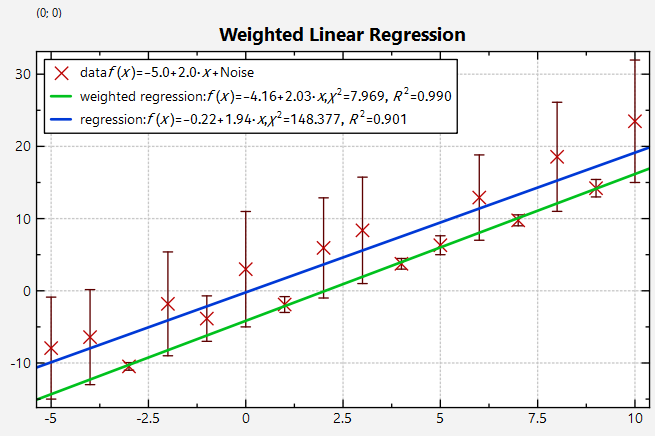
Weighted Linear Regression
Another option to react to measurement errors is to take these into account when calculating the regression. To do so, you can use weighted regression that uses the measurement errors as inverse weights. This algorithm is implemented in the function jkqtpstatLinearWeightedRegression().
First we generate again a set of datapoints (x,y), which scatter randomly around a linear function. In addition we calculate an "error" err for each datapoint:
std::random_device rd; // random number generators:
std::mt19937 gen{rd()};
std::uniform_real_distribution<> de{0.5,1.5};
std::uniform_int_distribution<> ddecide{0,4};
double a0=-5;
double b0=2;
size_t colWLinX=datastore1->addColumn("wlin data, x");
size_t colWLinY=datastore1->addColumn("wlin data, y");
size_t colWLinE=datastore1->addColumn("wlin data, errors");
for (double x=-5; x<=10; x++) {
double factor=1;
if (ddecide(gen)==4) {
factor=4;
}
const double err=de(gen)*factor;
datastore1->appendToColumn(colWLinX, x);
datastore1->appendToColumn(colWLinY, a0+b0*x+err);
datastore1->appendToColumn(colWLinE, 1.0/err);
}
We use distribution de to draw deviations from the ideal linear function from the range 0.5...1.5. then - for good measure - we use a second distribution ddecide (dice tossing) to select a few datapoints to have a 4-fold increased error.
Finally we visualize this data with a simple scatter graph with error indicators:
JKQTPXYLineErrorGraph* graphE;
plot2->addGraph(graphE=new JKQTPXYLineErrorGraph(plot2));
graphE->setXYColumns(colWLinX, colWLinY);
graphE->setYErrorColumn(static_cast<int>(colWLinE));
graphE->setDrawLine(false);
graphE->setTitle("data");
Now we can caluate the regression line (i.e. the two regression coefficients a and b of the function \c f(x)=a+b*x) using the function jkqtpstatLinearWeightedRegression() from the [statisticslibrary]:
double coeffA=0, coeffB=0;
jkqtpstatLinearWeightedRegression(datastore1->begin(colWLinX), datastore1->end(colWLinX),
datastore1->begin(colWLinY), datastore1->end(colWLinY),
datastore1->begin(colWLinE), datastore1->end(colWLinE),
coeffA, coeffB, false, false,
&jkqtp_inversePropSaveDefault<double>);
Note that in addition to the three data-columns we also provided a C++ functor jkqtp_inversePropSaveDefault(), which calculates 1/error. This is done, because the function jkqtpstatLinearWeightedRegression() uses the data from the range datastore1->begin(colWLinE) ... datastore1->end(colWLinE) directly as weights, but we calculated errors, which are inversely proportional to the weight of each data point when solving the least squares problem, as data points with larger errors should be weighted less than thos with smaller errors (outliers).
Again these two steps can be simplified using an "adaptor":
jkqtpstatAddLinearWeightedRegression(plot1->getPlotter(),
datastore1->begin(colLinX), datastore1->end(colLinX),
datastore1->begin(colLinY), datastore1->end(colLinY),
datastore1->begin(colWLinE), datastore1->end(colWLinE),
&coeffA, &coeffB, false, false,
&jkqtp_inversePropSaveDefault<double>);
... or even shorter:
jkqtpstatAddLinearWeightedRegression(graphD);
Here the x- and y-columns from the JKQTPXYGraph-based graph graphE (see above) and the weights from the error column of graphE are used as datasources for the plot. This function implicitly uses the function jkqtp_inversePropSaveDefault() to convert plot errors to weights, as it is already clear that we are dealing with errors rather than direct weights.
The plot resulting from any of the variants above looks like this:
For this plot we also added a call to
jkqtpstatAddLinearRegression(graphE);
which performs a simple non-weighted regression. The difference between the two resulting linear functions (blue: simple regression, green: weighted regression) demonstrates the influence of the weighting.
Linearizable Regression Models
In addition to the simple linear regression model f(x)=a+b*x, it is also possible to fit a few non-linear models by transforming the data:
- power-law function
f(x)=a*x^b, which is a linear function in a log(x)-log(y)-plot - exponential function
f(x)=a*exp(b*x), which is a linear function in a x-log(y)-plot - logarithm function
f(x)=a+b*ln(x), which is a linear function in a exp(x)-y-plot The available models are defined in the enumJKQTPStatRegressionModelType. And there exists a functionjkqtpStatGenerateRegressionModel(), which returns a C++-functor representing the function.
To demonstrate these fitting options, we first generate data from an exponential and a power-law model. Note that we also add normally distributed errors, but in order to ensure that we do not obtain y-values <0, we use loops that draw normally distributed random numbers, until this condition is met:
std::random_device rd; // random number generators:
std::mt19937 gen{rd()};
std::normal_distribution<> d1{0,1};
double a0_powerlaw=20;
double b0_powerlaw=0.25;
double a0_exp=5;
double b0_exp=0.5;
size_t colNLLinX=datastore1->addColumn("non-lin data, x");
size_t colNLLinYExp=datastore1->addColumn("non-lin data, y, exponential model");
size_t colNLLinYPow=datastore1->addColumn("non-lin data, y, power-law model");
auto model_powerlaw=jkqtpStatGenerateRegressionModel(JKQTPStatRegressionModelType::PowerLaw);
auto model_exp=jkqtpStatGenerateRegressionModel(JKQTPStatRegressionModelType::Exponential);
for (double x=0.1; x<=10; x+=0.5) {
datastore1->appendToColumn(colNLLinX, x);
double ypow=model_powerlaw(x, a0_powerlaw, b0_powerlaw)+d1(gen);
while (ypow<0) {
ypow=model_powerlaw(x, a0_powerlaw, b0_powerlaw)+d1(gen);
}
datastore1->appendToColumn(colNLLinYPow, ypow);
double yexp=model_exp(x, a0_exp, b0_exp)+d1(gen);
while (yexp<0) {
yexp=model_exp(x, a0_exp, b0_exp)+d1(gen);
}
datastore1->appendToColumn(colNLLinYExp, yexp);
}
The generated data is visualized with scatter-plots:
JKQTPXYLineGraph* graphD_powerlaw;
plot5->addGraph(graphD_powerlaw=new JKQTPXYLineGraph(plot5));
graphD_powerlaw->setXYColumns(colNLLinX, colNLLinYPow);
graphD_powerlaw->setDrawLine(false);
graphD_powerlaw->setTitle(QString("data $%1+\\mathcal{N}(0,1)$").arg(jkqtpstatRegressionModel2Latex(JKQTPStatRegressionModelType::PowerLaw, a0_powerlaw, b0_powerlaw)));
JKQTPXYLineGraph* graphD_exp;
plot4->addGraph(graphD_exp=new JKQTPXYLineGraph(plot4));
graphD_exp->setXYColumns(colNLLinX, colNLLinYExp);
graphD_exp->setDrawLine(false);
graphD_exp->setTitle(QString("data $%1+\\mathcal{N}(0,1)$").arg(jkqtpstatRegressionModel2Latex(JKQTPStatRegressionModelType::Exponential, a0_exp, b0_exp)));
Now we can fit the regression models using jkqtpstatRegression(), which receives the model type as first parameter:
double cA=0, cB=0;
JKQTPXFunctionLineGraph* gFunc;
jkqtpstatRegression(JKQTPStatRegressionModelType::Exponential, datastore1->begin(colNLLinX), datastore1->end(colNLLinX), datastore1->begin(colNLLinYExp), datastore1->end(colNLLinYExp), cA, cB);
plot4->addGraph(gFunc=new JKQTPXFunctionLineGraph(plot4));
gFunc->setPlotFunctionFunctor(jkqtpStatGenerateRegressionModel(JKQTPStatRegressionModelType::Exponential, cA, cB));
gFunc->setTitle(QString("regression: $%1$").arg(jkqtpstatRegressionModel2Latex(JKQTPStatRegressionModelType::Exponential, cA, cB)));
cA=0; cB=0;
jkqtpstatRegression(JKQTPStatRegressionModelType::PowerLaw, datastore1->begin(colNLLinX), datastore1->end(colNLLinX), datastore1->begin(colNLLinYPow), datastore1->end(colNLLinYPow), cA, cB);
plot5->addGraph(gFunc=new JKQTPXFunctionLineGraph(plot5));
gFunc->setPlotFunctionFunctor(jkqtpStatGenerateRegressionModel(JKQTPStatRegressionModelType::PowerLaw, cA, cB));
gFunc->setTitle(QString("regression: $%1$").arg(jkqtpstatRegressionModel2Latex(JKQTPStatRegressionModelType::PowerLaw, cA, cB)));
The regression models can be plotted using a JKQTPXFunctionLineGraph. the fucntion to plot is again generated by calling jkqtpStatGenerateRegressionModel(), but now with the parameters determined above the respective lines. Note that jkqtpstatRegressionModel2Latex() outputs the model as LaTeX string, which can be used as plot label.
The resulting plot looks like this:
Of course also "adaptors" exist that allow to perform the steps above in a single function call:
jkqtpstatAddRegression(plot4->getPlotter(), JKQTPStatRegressionModelType::Exponential, datastore1->begin(colNLLinX), datastore1->end(colNLLinX), datastore1->begin(colNLLinYExp), datastore1->end(colNLLinYExp));
jkqtpstatAddRegression(plot5->getPlotter(), JKQTPStatRegressionModelType::PowerLaw, datastore1->begin(colNLLinX), datastore1->end(colNLLinX), datastore1->begin(colNLLinYPow), datastore1->end(colNLLinYPow));
... or even shorter:
jkqtpstatAddRegression(graphD_exp, JKQTPStatRegressionModelType::Exponential);
jkqtpstatAddRegression(graphD_powerlaw, JKQTPStatRegressionModelType::PowerLaw);
Also note that we used the function jkqtpstatRegression() above, which performs a linear regression (internally uses jkqtpstatLinearRegression()). But there also exist variants for robust IRLS regression adn weighted regression:
jkqtpstatRobustIRLSRegression()/jkqtpstatAddRobustIRLSRegression()jkqtpstatWeightedRegression()/jkqtpstatAddWeightedRegression()
Polynom Fitting
Finally the [statisticslibrary] also supports one option for non-linear model fitting, namely fitting of polynomial models. This is implemented in the function jkqtpstatPolyFit().
To demonstrate this function we first generate data from a poylnomial model (with gaussian noise):
std::random_device rd; // random number generators:
std::mt19937 gen{rd()};
std::normal_distribution<> d1{0,50};
std::vector<double> pPoly {1,2,-2,0.5};
size_t colPolyX=datastore1->addColumn("polynomial data, x");
size_t colPolyY=datastore1->addColumn("polynomial data, y");
for (double x=-10; x<=10; x++) {
datastore1->appendToColumn(colPolyX, x);
datastore1->appendToColumn(colPolyY, jkqtp_polyEval(x, pPoly.begin(), pPoly.end())+d1(gen));
}
The function jkqtp_polyEval() is used to evaluate a given polynomial (coefficients in pPoly) at a position x.
The generated data is visualized with scatter-plots:
JKQTPXYLineGraph* graphP;
plot6->addGraph(graphP=new JKQTPXYLineGraph(plot6));
graphP->setXYColumns(colPolyX, colPolyY);
graphP->setDrawLine(false);
graphP->setTitle(QString("data $%1+\\mathcal{N}(0,50)$").arg(jkqtp_polynomialModel2Latex(pPoly.begin(), pPoly.end())));
Here the function jkqtp_polynomialModel2Latex() generates a string from a polynomial model.
Now we can call jkqtpstatPolyFit() to fit different polynomial regression models to the data:
for (size_t p=0; p<=5; p++) {
std::vector<double> pFit;
JKQTPXFunctionLineGraph* gPoly;
jkqtpstatPolyFit(datastore1->begin(colPolyX), datastore1->end(colPolyX), datastore1->begin(colPolyY), datastore1->end(colPolyY), p, std::back_inserter(pFit));
plot6->addGraph(gPoly=new JKQTPXFunctionLineGraph(plot6));
gPoly->setPlotFunctionFunctor(jkqtp_generatePolynomialModel(pFit.begin(), pFit.end()));
gPoly->setTitle(QString("regression: $%1$").arg(jkqtp_polynomialModel2Latex(pFit.begin(), pFit.end())));
}
Each model is also ploted using a JKQTPXFunctionLineGraph. The plot function assigned to these JKQTPXFunctionLineGraph is generated by calling jkqtp_generatePolynomialModel(), which returns a C++-functor for a polynomial.
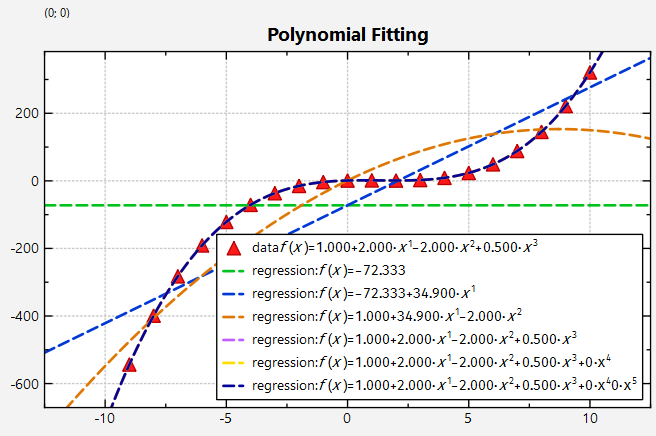
The resulting plots look like this (without added gaussian noise):
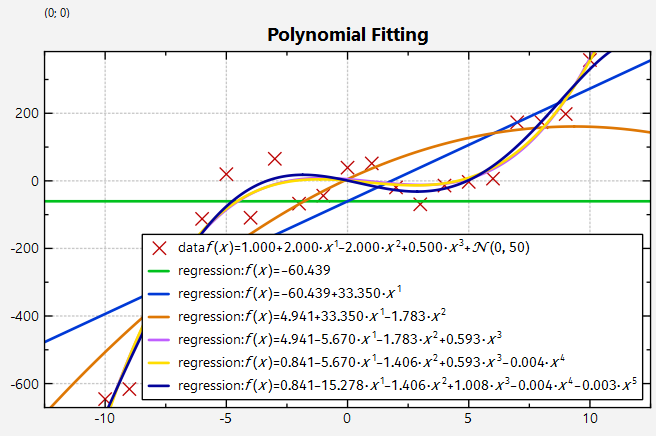
... and with added gaussian noise:
Of course also the "adaptor" shortcuts are available:
for (size_t p=0; p<=5; p++) {
jkqtpstatAddPolyFit(plot6->getPlotter(), datastore1->begin(colPolyX), datastore1->end(colPolyX), datastore1->begin(colPolyY), datastore1->end(colPolyY), p);
jkqtpstatAddPolyFit(graphP, p);
}
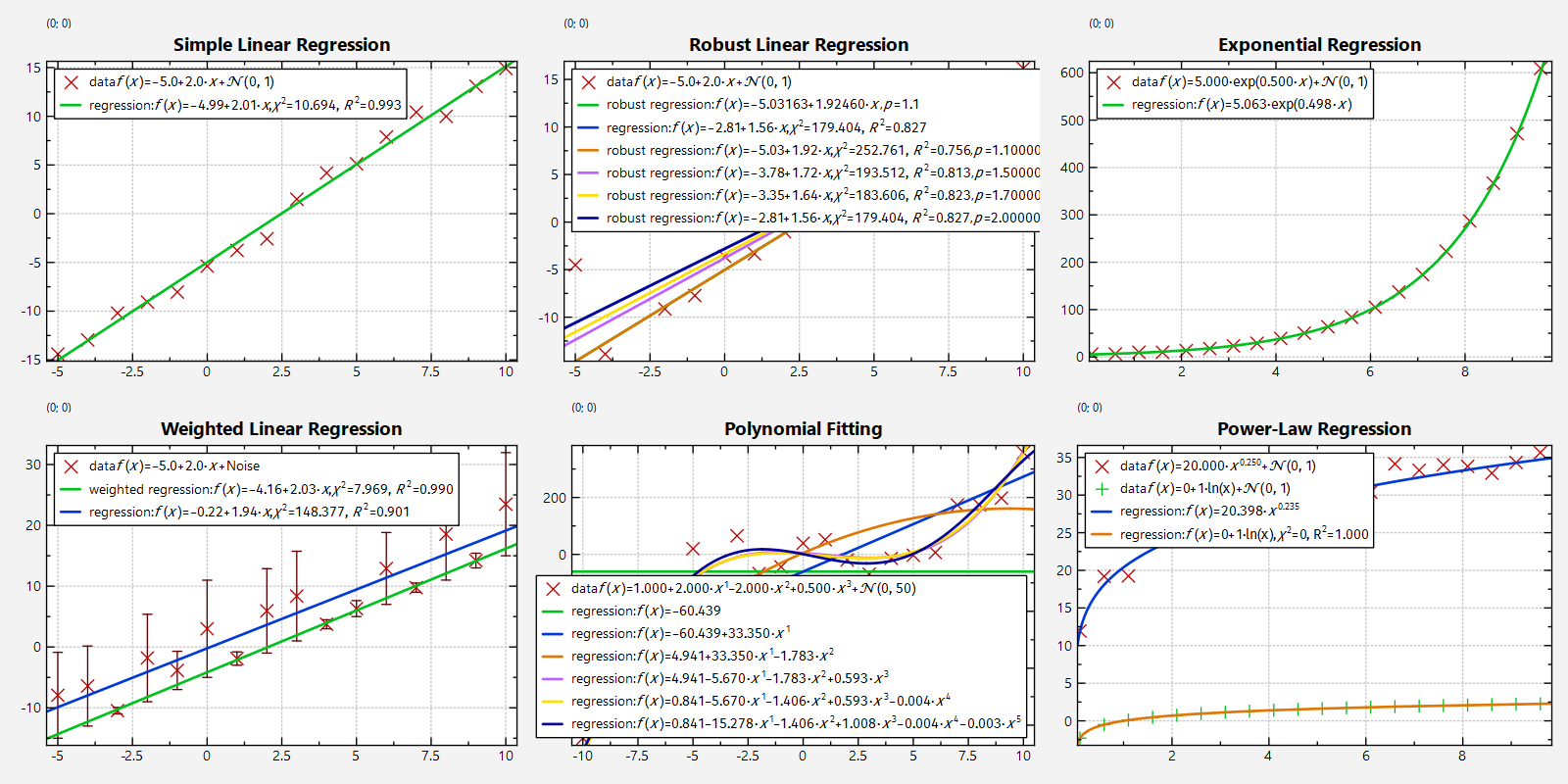
Screenshot of the full Program
The output of the full test program datastore_regression.cpp looks like this: