| .. | ||
| CMakeLists.txt | ||
| datastore_statistics_2d_and_lib.pro | ||
| datastore_statistics_2d.cpp | ||
| datastore_statistics_2d.pro | ||
| README.md | ||
Tutorial (JKQTPDatastore): Advanced 2-Dimensional Statistics with JKQTPDatastore
[JKQTPlotterBasicJKQTPDatastore]: @ref JKQTPlotterBasicJKQTPDatastore "Basic Usage of JKQTPDatastore" [JKQTPlotterBasicJKQTPDatastoreIterators]: @ref JKQTPlotterBasicJKQTPDatastoreIterators "Iterator-Based usage of JKQTPDatastore" [JKQTPlotterBasicJKQTPDatastoreStatistics]: @ref JKQTPlotterBasicJKQTPDatastoreStatistics "Advanced 1-Dimensional Statistics with JKQTPDatastore" [JKQTPlotterBasicJKQTPDatastoreRegression]: @ref JKQTPlotterBasicJKQTPDatastoreRegression "Regression Analysis (with the Statistics Library)" [JKQTPlotterBasicJKQTPDatastoreStatisticsGroupedStat]: @ref JKQTPlotterBasicJKQTPDatastoreStatisticsGroupedStat "1-Dimensional Group Statistics with JKQTPDatastore" [JKQTPlotterBasicJKQTPDatastoreStatistics2D]: @ref JKQTPlotterBasicJKQTPDatastoreStatistics2D "Advanced 2-Dimensional Statistics with JKQTPDatastore" [statisticslibrary]: @ref jkqtptools_math_statistics "JKQTPlotter Statistics Library"
This tutorial project (see ./examples/datastore_statistics_2d/) explains several advanced functions of JKQTPDatastore in combination with the statisticslibrary conatined in JKQTPlotter.
Note that there are additional tutorial explaining other aspects of data mangement in JKQTPDatastore:
- [JKQTPlotterBasicJKQTPDatastore]
- [JKQTPlotterBasicJKQTPDatastoreIterators]
- [JKQTPlotterBasicJKQTPDatastoreStatistics]
- [JKQTPlotterBasicJKQTPDatastoreRegression]
- [JKQTPlotterBasicJKQTPDatastoreStatisticsGroupedStat]
- [JKQTPlotterBasicJKQTPDatastoreStatistics2D]
[TOC]
The source code of the main application can be found in datastore_statistics_2d.cpp.
This tutorial cites only parts of this code to demonstrate different ways of working with data for the graphs.
Generating different sets of random numbers
The code segments below will fill different instances of JKQTPlotter with different statistical plots. All these plots are based on either of two sets of random number pairs (i.e. x/y-locations) generated as shown here:
size_t randomdatacolx_small=datastore1->addColumn("random data, x");
size_t randomdatacoly_small=datastore1->addColumn("random data, y");
size_t randomdatacoldist_small=datastore1->addColumn("random data, distribution/class");
size_t randomdatacolx=datastore1->addColumn("random data, x");
size_t randomdatacoly=datastore1->addColumn("random data, y");
size_t randomdatacoldist=datastore1->addColumn("random data, distribution/class");
// random number generators:
std::random_device rd;
std::mt19937 gen{rd()};
std::uniform_int_distribution<> ddecide(0,2);
std::normal_distribution<> d1x{5,3};
std::normal_distribution<> d1y{5,1};
std::normal_distribution<> d2x{10,2};
std::normal_distribution<> d2y{10,5};
for (size_t i=0; i<500; i++) {
double rx=0,ry=0;
const int decide=ddecide(gen);
if (decide==0) {
rx=d1x(gen);
ry=d1y(gen);
} else {
rx=d2x(gen);
ry=d2y(gen);
}
if (i<150) {
datastore1->appendToColumn(randomdatacolx_small, rx);
datastore1->appendToColumn(randomdatacoly_small, ry);
datastore1->appendToColumn(randomdatacoldist_small, std::min(1,decide));
}
datastore1->appendToColumn(randomdatacolx, rx);
datastore1->appendToColumn(randomdatacoly, ry);
datastore1->appendToColumn(randomdatacoldist, std::min(1,decide));
}
The columns randomdatacolx and randomdatacoly will contain 500 random numbers. Each one is drawn either from the normal distributions d1x/d1y, or d2x/d2y. The decision, which of the two to use is based on the result of a third random distribution ddecide, which only returns 0, 1 or 2 (d1x/d1y is chosen for ddecide==0). The column randomdatacoldist finally encodes which pair of distributions was chosen. The three columns randomdatacolx_small, randomdatacoly_small and randomdatacoldist_small represent a subset of the first 150 numbers from the full dataset.
The columns are generated empty by calling JKQTPDatastore::addColumn() with only a name. Then the actual values are added by calling JKQTPDatastore::appendToColumn().
The datasets generated above can be plotted using a simple scatterplot (here shown for the full dataset only):
JKQTPXYParametrizedScatterGraph* gDataHist;
plothist->addGraph(gDataHist=new JKQTPXYParametrizedScatterGraph(plothist));
gDataHist->setXYColumns(randomdatacolx,randomdatacoly);
gDataHist->setSymbolColumn(randomdatacoldist);
QMap<double, JKQTPGraphSymbols> mapped;
mapped[0]=JKQTPGraphSymbols::JKQTPCross;
mapped[1]=JKQTPGraphSymbols::JKQTPPlus;
gDataHist->setMappedSymbolColumnFunctor(mapped);
gDataHist->setSymbolSize(5);
gDataHist->setSymbolColor(QColorWithAlphaF(QColor("red"), 0.7));
gDataHist->setDrawLine(false);
gDataHist->setTitle(QString("random data, $N="+QString::number(datastore1->getRows(randomdatacoldist))+"$"));
In addition to get an idea of the used distributions, we can add two ellipses indicating the (doubled) standard deviations of the two distributions:
// 2.3. to visualize the initial distributions, we draw an ellipse indicating the
// variance of the distributions
JKQTPGeoEllipse* gEll1Hist;
JKQTPGeoEllipse* gEll2Hist;
plothist->addGraph(gEll1Hist=new JKQTPGeoEllipse(plothist, d1x.mean(), d1y.mean(),d1x.stddev()*2.0,d1y.stddev()*2.0));
plothist->addGraph(gEll2Hist=new JKQTPGeoEllipse(plothist, d2x.mean(), d2y.mean(),d2x.stddev()*2.0,d2y.stddev()*2.0));
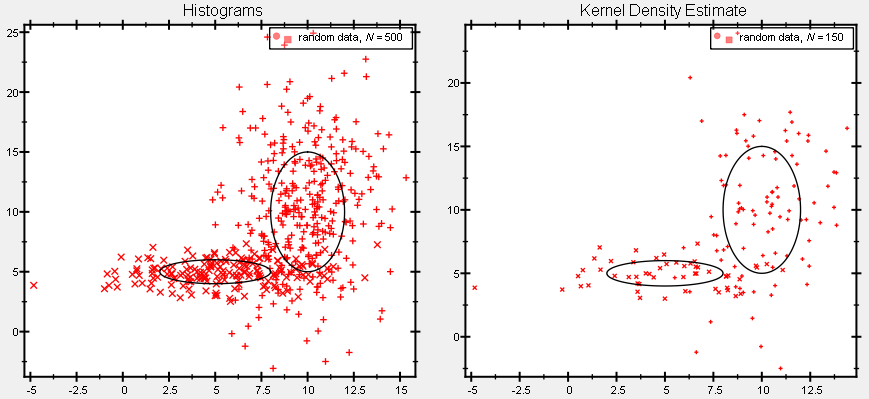
The resulting plot looks like this:
Marginal Statistics
To explore the statistical properties of a 2D dataset, it is often useful to draw the marginal histograms, i.e. the histograms of one of the two variables. To do so, we use the function jkqtpstatAddHHistogram1DAutoranged() and jkqtpstatAddVHistogram1DAutoranged() that were introduced in [JKQTPlotterBasicJKQTPDatastoreStatistics] and are explained in detail there:
jkqtpstatAddHHistogram1DAutoranged(plothistBottom->getPlotter(), datastore1->begin(randomdatacolx), datastore1->end(randomdatacolx), 1.0, true);
jkqtpstatAddVHistogram1DAutoranged(plothistLeft->getPlotter(), datastore1->begin(randomdatacoly), datastore1->end(randomdatacoly), 1.0, true);
Note that the plots are put into JKQTPlotter-instances plothistBottom and plothistLeft. These are put into a global QGridSizer just below and left of the main histogram plot plothist. The axes of these plots are linked to the main plot, so zooming one affects the other plot too and their axes are inverted, so the drawn histogram elongates to the left and to the bottom (starting with 0 at the main plot plothist):
QGridLayout* lay;
JKQTPlotter* plothist=new JKQTPlotter(&mainWidget);
lay->addWidget(plothist,0,1);
plothist->getPlotter()->setPlotLabel("Histograms");
JKQTPDatastore* datastore1=plothist->getDatastore();
JKQTPlotter* plothistLeft=new JKQTPlotter(datastore1, &mainWidget);
lay->addWidget(plothistLeft,0,0);
JKQTPlotter* plothistBottom=new JKQTPlotter(datastore1, &mainWidget);
lay->addWidget(plothistBottom,1,1);
plothistLeft->synchronizeYToMaster(plothist);
plothistLeft->setAbsoluteX(0,1);
plothistLeft->getXAxis()->setInverted(true);
plothistLeft->getXAxis()->setShowZeroAxis(false);
plothistLeft->getYAxis()->setShowZeroAxis(false);
plothistLeft->getYAxis()->setDrawMode1(JKQTPCADMLine);
plothistLeft->getYAxis()->setDrawMode2(JKQTPCADMLineTicks);
plothistLeft->setGrid(false);
plothistBottom->synchronizeXToMaster(plothist);
plothistBottom->setAbsoluteY(0,1);
plothistBottom->getYAxis()->setInverted(true);
plothistBottom->getXAxis()->setShowZeroAxis(false);
plothistBottom->getYAxis()->setShowZeroAxis(false);
plothistBottom->getXAxis()->setDrawMode1(JKQTPCADMLine);
plothistBottom->getXAxis()->setDrawMode2(JKQTPCADMLineTicks);
plothistBottom->setGrid(false);
plothistBottom->setMousePositionShown(false);
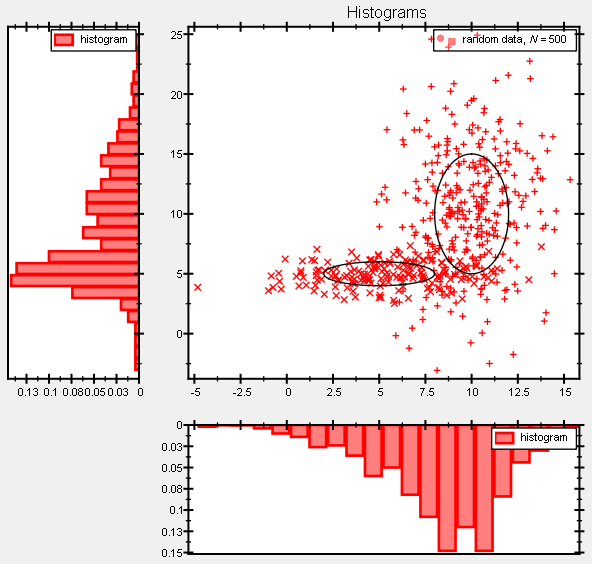
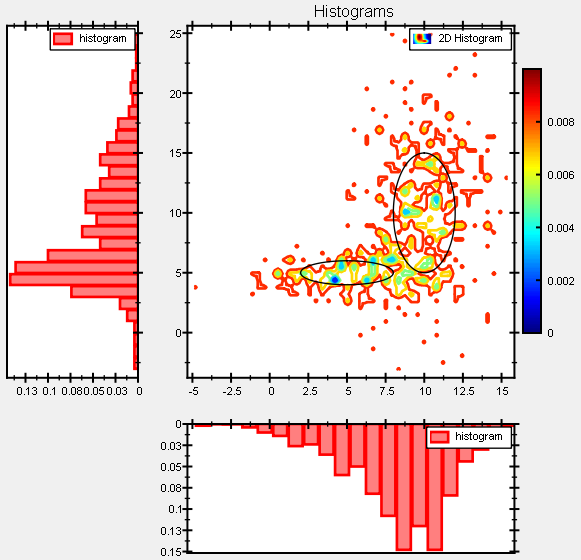
This results in a graph like this:
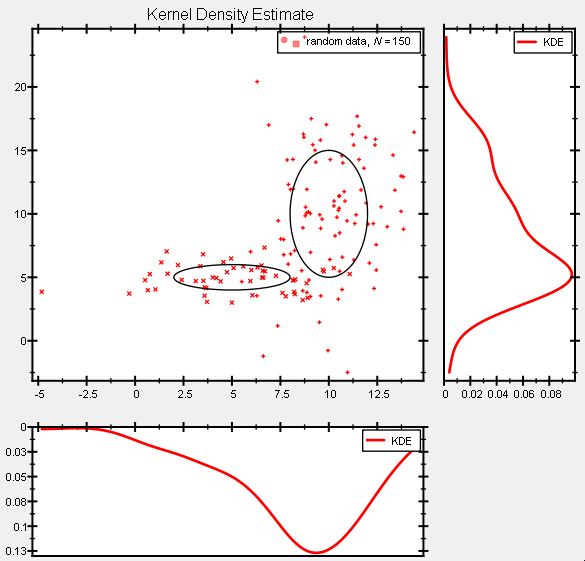
With the same method, also marginal Kernel Density Estimates can be drawn:
double bwx=jkqtpstatEstimateKDEBandwidth(datastore1->begin(randomdatacolx_small), datastore1->end(randomdatacolx_small));
jkqtpstatAddHKDE1DAutoranged(plotkdeBottom->getPlotter(), datastore1->begin(randomdatacolx_small), datastore1->end(randomdatacolx_small), 0.01, &jkqtpstatKernel1DGaussian, bwx);
double bwy=jkqtpstatEstimateKDEBandwidth(datastore1->begin(randomdatacoly_small), datastore1->end(randomdatacoly_small));
jkqtpstatAddVKDE1DAutoranged(plotkdeRight->getPlotter(), datastore1->begin(randomdatacoly_small), datastore1->end(randomdatacoly_small), 0.01, &jkqtpstatKernel1DGaussian, bwy);
2D Histogram
Calculating 2D-Histograms is implemented in jkqtpstatHistogram2D() from the [statisticslibrary]. This functions calculates a histogram on a given grid with the first bin at xmin,ymin and the last bin at xmax,ymax, containing Nx,Ny bins in x-/y-direction. You can use the result to fill new image column (with Nx columns and Ny rows) in a JKQTPDatastore, which can then be used to draw the histogram.
First we have to determine the x- and y-range of data and calculate the number of bins from these:
double xmin=0, xmax=0;
double ymin=0, ymax=0;
jkqtpstatMinMax(datastore1->begin(randomdatacolx), datastore1->end(randomdatacolx), xmin,xmax);
jkqtpstatMinMax(datastore1->begin(randomdatacoly), datastore1->end(randomdatacoly), ymin,ymax);
size_t Nx=jkqtp_ceilTo<size_t>((xmax-xmin)/2.0);
size_t Ny=jkqtp_ceilTo<size_t>((ymax-ymin)/2.0);
Now we can add the image column
size_t histcol=datastore1->addImageColumn(Nx, Ny, "2d histogram");
and calculate the histogram:
jkqtpstatHistogram2D(datastore1->begin(randomdatacolx), datastore1->end(randomdatacolx), datastore1->begin(randomdatacoly), datastore1->end(randomdatacoly),
datastore1->begin(histcol),
xmin, xmax, ymin, ymax,
Nx, Ny, true);
Finally the histogram is drawn using a JKQTPColumnMathImage:
JKQTPColumnMathImage* gHist;
plothist->addGraph(gHist=new JKQTPColumnMathImage(plothist));
gHist->setImageColumn(static_cast<int>(histcol));
gHist->setX(xmin);
gHist->setY(ymin);
gHist->setWidth(xmax-xmin);
gHist->setHeight(ymax-ymin);
gHist->setTitle("2D Histogram");
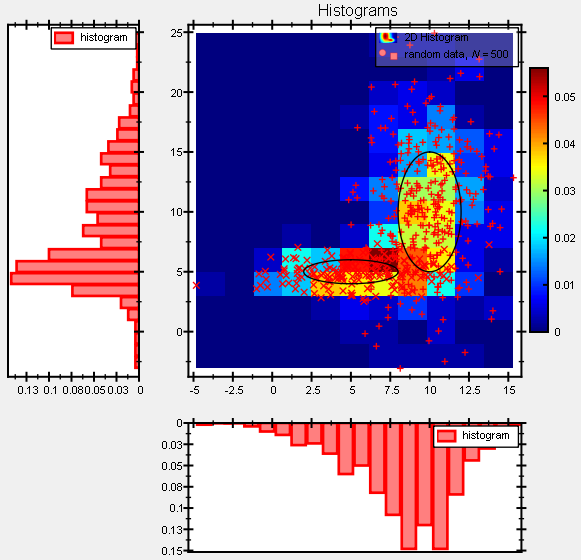
The resulting image plot looks like this:
There is also an "adaptor" which significanty reduce the amount of coude you have to type (i.e. it replaces all the code above):
jkqtpstatAddHistogram2DImage(plothist->getPlotter(), datastore1->begin(randomdatacolx), datastore1->end(randomdatacolx), datastore1->begin(randomdatacoly), datastore1->end(randomdatacoly), Nx, Ny, true);
jkqtpstatAddHistogram2DContour(plothist->getPlotter(), datastore1->begin(randomdatacolx), datastore1->end(randomdatacolx), datastore1->begin(randomdatacoly), datastore1->end(randomdatacoly), Nx, Ny, true);
These differ in the type of plot that is added jkqtpstatAddHistogram2DImage() adds an image graph (JKQTPColumnMathImage) and jkqtpstatAddHistogram2DContour() adds a contour plot (JKQTPColumnContourPlot). A contour plot may look like this:
Kernel Density Estimates (KDE)
Especially when only few samples from a distribution are available, histograms are not good at representing the underlying data distribution. In such cases, Kernel Density Estimates (KDE) can help, which are basically a smoothed variant of a histogram. The [statisticslibrary] supports calculating them via e.g. jkqtpstatKDE2D():
This functions calculates a histogram on a given grid with the first bin at xmin,ymin and the last bin at xmax,ymax, containing Nx,Ny bins in x-/y-direction. You can use the result to fill new image column (with Nx columns and Ny rows) in a JKQTPDatastore, which can then be used to draw the histogram.
First we have to determine the x- and y-range of data and calculate the number of bins from these:
double xmin=0, xmax=0;
double ymin=0, ymax=0;
jkqtpstatMinMax(datastore1->begin(randomdatacolx_small), datastore1->end(randomdatacolx_small), xmin,xmax);
jkqtpstatMinMax(datastore1->begin(randomdatacoly_small), datastore1->end(randomdatacoly_small), ymin,ymax);
Nx=jkqtp_ceilTo<size_t>((xmax-xmin)/0.1);
Ny=jkqtp_ceilTo<size_t>((ymax-ymin)/0.1);
We can also estimate the KDE-bandwidth for both directions now:
bwx=jkqtpstatEstimateKDEBandwidth2D(datastore1->begin(randomdatacolx_small), datastore1->end(randomdatacolx_small));
bwy=jkqtpstatEstimateKDEBandwidth2D(datastore1->begin(randomdatacoly_small), datastore1->end(randomdatacoly_small));
Now we can add the image column
size_t kdecol=datastore1->addImageColumn(Nx, Ny, "2d KDE");
and calculate the histogram:
jkqtpstatKDE2D(datastore1->begin(randomdatacolx_small), datastore1->end(randomdatacolx_small), datastore1->begin(randomdatacoly_small), datastore1->end(randomdatacoly_small),
datastore1->begin(kdecol),
xmin, xmax, ymin, ymax, Nx, Ny,
&jkqtpstatKernel2DGaussian, bwx, bwy);
Finally the histogram is drawn using a JKQTPColumnMathImage:
JKQTPColumnMathImage* gKDE;
plotkde->addGraph(gKDE=new JKQTPColumnMathImage(plotkde));
gKDE->setImageColumn(static_cast<int>(kdecol));
gKDE->setX(xmin);
gKDE->setY(ymin);
gKDE->setWidth(xmax-xmin);
gKDE->setHeight(ymax-ymin);
gKDE->setTitle("2D KDE");
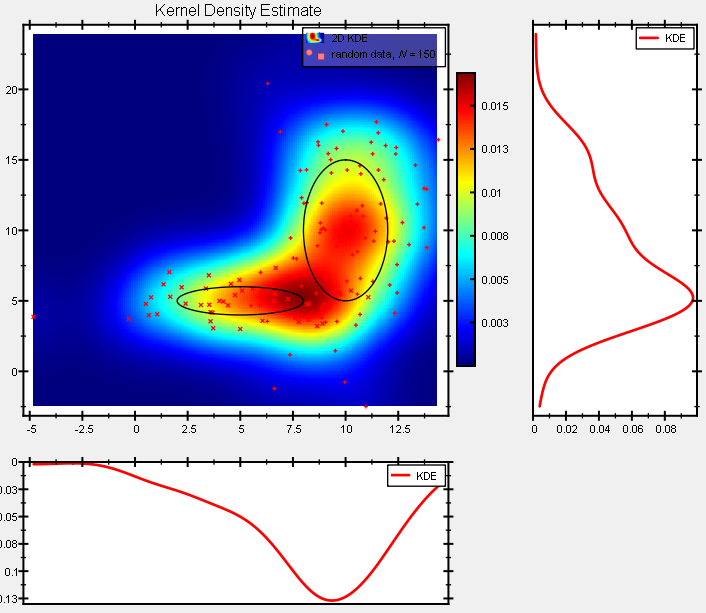
The resulting plot image looks like this:
Note that calculating a KDE is a rather time-consuming task. The KDE in the image above took about 8s to calculate (from 150 datapairs and on a 193*267 pixel grid), whereas the corresponding histogram took only 1ms to calculate!
There is also an "adaptor" which significanty reduce the amount of coude you have to type (i.e. it replaces all the code above):
jkqtpstatAddKDE2DImage(plotkde->getPlotter(), datastore1->begin(randomdatacolx_small), datastore1->end(randomdatacolx_small), datastore1->begin(randomdatacoly_small), datastore1->end(randomdatacoly_small), Nx, Ny, &jkqtpstatKernel2DGaussian, bwx, bwy);
jkqtpstatAddKDE2DContour(plotkde->getPlotter(), datastore1->begin(randomdatacolx_small), datastore1->end(randomdatacolx_small), datastore1->begin(randomdatacoly_small), datastore1->end(randomdatacoly_small), Nx, Ny, &jkqtpstatKernel2DGaussian, bwx, bwy);
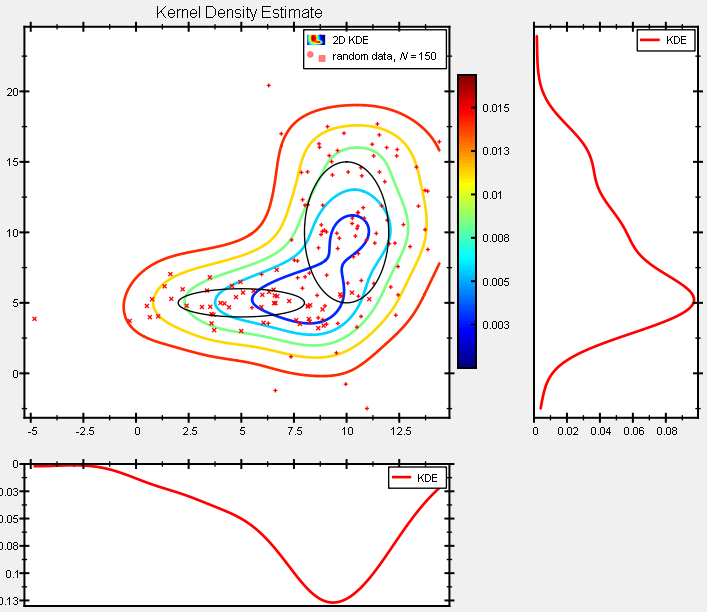
These differ in the type of plot that is added jkqtpstatAddKDE2DImage() adds an image graph (JKQTPColumnMathImage) and jkqtpstatAddKDE2DContour() adds a contour plot (JKQTPColumnContourPlot). the first is shown in the screenshot above, the latter looks like this:
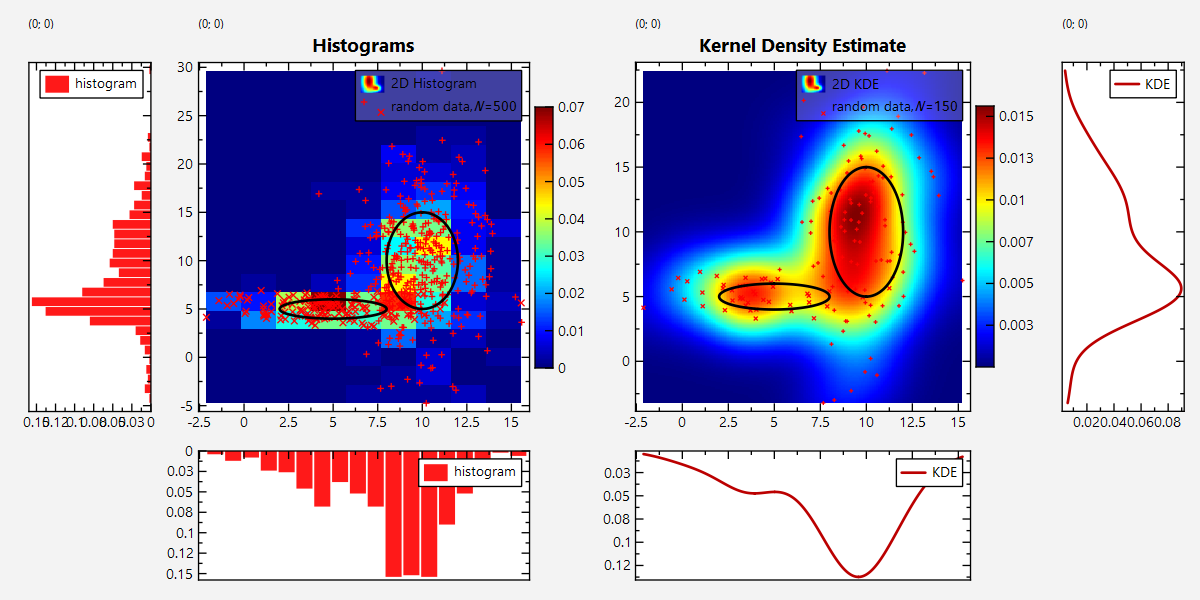
Screenshot of the full Program
The output of the full test program datastore_statistics_2d.cpp looks like this: