mirror of
https://github.com/jkriege2/JKQtPlotter.git
synced 2025-01-23 22:22:11 +08:00
| .. | ||
| README.md | ||
| test_distributionplot_and_lib.pro | ||
| test_distributionplot.cpp | ||
| test_distributionplot.pro | ||
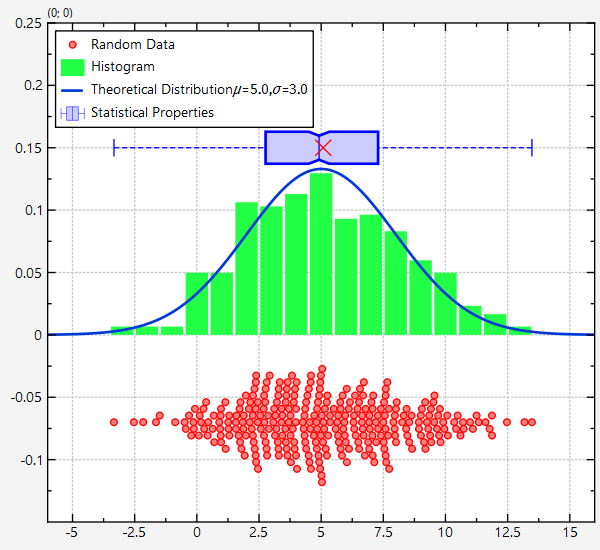
Example (JKQTPlotter): Plotting a Statistical Distribution of Data
This project (see test_distributionplot demonstrates how to combine several different graphs and geometric elements to show a set of random values and their statistics.
The source code of the main application is (see test_distributionplot.cpp.
After adding all necessary data to the JKQTDatastore:
// 1. create a plotter window and get a pointer to the internal datastore (for convenience)
JKQTPlotter plot;
plot.getPlotter()->setUseAntiAliasingForGraphs(true); // nicer (but slower) plotting
plot.getPlotter()->setUseAntiAliasingForSystem(true); // nicer (but slower) plotting
plot.getPlotter()->setUseAntiAliasingForText(true); // nicer (but slower) text rendering
JKQTPDatastore* ds=plot.getDatastore();
// 2. now we create random values drawn from a gaussian distribution
QVector<double> RANDVAL; // will store the values themselves
std::map<int, double> hist; // is used to calculate the histogram of the data
for (int i=-5; i<=15; i++) hist[i]=0;
std::random_device rd; // random number generators:
std::mt19937 gen{rd()};
// draw 301 random values from a gaussian distribution around 5 with width 3
const double th_mean=5;
const double th_std=3;
std::normal_distribution<> d{th_mean,th_std};
size_t NDATA=301;
double sum=0;
double square_sum=0;
for (size_t i=0; i<NDATA; i++) {
const double v=d(gen);
RANDVAL<<v; // store data
++hist[std::round(v)]; // calculate histogram
// accumulate data for statistics:
sum+=v;
square_sum+=(v*v);
}
// normalize histogram
for (auto& hi: hist) {
hi.second=hi.second/static_cast<double>(NDATA);
}
// sort random data in order to calculate the statistical properties:
qSort(RANDVAL);
const double rndMean=sum/static_cast<double>(NDATA);
const double rndMin=RANDVAL.first();
const double rndMax=RANDVAL.last();
const double rndMedian=RANDVAL[RANDVAL.size()/2];
const double rndQ25=RANDVAL[RANDVAL.size()/4];
const double rndQ75=RANDVAL[RANDVAL.size()*3/4];
const double rndMedianConfidence=2.0*1.57*fabs(rndQ75-rndQ25)/sqrt(static_cast<double>(NDATA));
// 3. make data available to JKQTPlotter by adding it to the internal datastore.
size_t columnRANDVAL=ds->addCopiedColumn(RANDVAL, "RANDVAL"); // copy random values
std::pair<size_t,size_t> columnHIST = ds->addCopiedMap(hist, "HIST_X", "HIST_Y"); // copy histogram
// 4. create a graph of horizontal boxplots:
JKQTPSingleColumnSymbolsGraph* graphRANDVALS=new JKQTPSingleColumnSymbolsGraph(&plot);
graphRANDVALS->setDataColumn(columnRANDVAL);
// draw data as symbols at (x,y)=(data,-0.07):
graphRANDVALS->setDataDirection(JKQTPSingleColumnSymbolsGraph::DataDirection::X);
graphRANDVALS->setPosition(-0.07);
// data should scatter around position=-0.07 with a width=0.08 (i.e. from position-width/2 ... position+width/2)
//graphRANDVALS->setWidth(0.08);
//graphRANDVALS->setPositionScatterStyle(JKQTPSingleColumnSymbolsGraph::RandomScatter);
// data should scatter around position=-0.07 in a BeeSwarmScatter-Plot
graphRANDVALS->setPositionScatterStyle(JKQTPSingleColumnSymbolsGraph::BeeSwarmScatter);
// choose small filled circles as symbols, JKQTPGraphSymbols::set their color:
graphRANDVALS->setSymbolType(JKQTPFilledCircle);
graphRANDVALS->setSymbolSize(5);
graphRANDVALS->setColor(QColor("red"));
graphRANDVALS->setFillColor(graphRANDVALS->getColor().lighter(180));
// set title:
graphRANDVALS->setTitle("Random Data");
// 5. draw the histogram as barchart:
JKQTPBarVerticalGraph* graphHIST=new JKQTPBarVerticalGraph(&plot);
graphHIST->setXColumn(columnHIST.first);
graphHIST->setYColumn(columnHIST.second);
// set title:
graphHIST->setTitle("Histogram");
// 6. draw the theoretical distribution as function graph:
JKQTPXFunctionLineGraph* graphTheoDist=new JKQTPXFunctionLineGraph(&plot);
// define the gaussian function used for the random number generator
graphTheoDist->setPlotFunctionFunctor([&th_mean,&th_std](double x) -> double {
return 1.0/(th_std*sqrt(2.0*M_PI))*exp(-0.5*(x-th_mean)*(x-th_mean)/th_std/th_std);
});
// set title:
graphTheoDist->setTitle(QString("Theoretical Distribution $\\mu=%1, \\sigma=%2$").arg(th_mean,0, 'f', 1).arg(th_std,0, 'f', 1));
// 7. create a graph of horizontal boxplots:
JKQTPBoxplotHorizontalElement* graphBoxPlot=new JKQTPBoxplotHorizontalElement(&plot);
graphBoxPlot->setPos(0.15);
graphBoxPlot->setMin(rndMin);
graphBoxPlot->setPercentile25(rndQ25);
graphBoxPlot->setMean(rndMean);
graphBoxPlot->setMedian(rndMedian);
graphBoxPlot->setMedianConfidenceIntervalWidth(rndMedianConfidence);
graphBoxPlot->setPercentile75(rndQ75);
graphBoxPlot->setMax(rndMax);
graphBoxPlot->setBoxWidthAbsolute(24);
graphBoxPlot->setMeanSize(16);
graphBoxPlot->setLineWidth(2);
graphBoxPlot->setTitle("Statistical Properties");
graphBoxPlot->setBoxplotColor(QColor("blue"), plot.getPlotter());
// make fill collor a lighter shade of the outline color
graphBoxPlot->setFillColor(graphBoxPlot->getLineColor().lighter(180));
// make whiskers dashed
graphBoxPlot->setWhiskerLineStyle(Qt::DashLine);
// 8. add the graphs to the plot, so it is actually displayed
plot.addGraph(graphRANDVALS);
plot.addGraph(graphHIST);
plot.addGraph(graphTheoDist);
plot.addGraph(graphBoxPlot);
// 9. autoscale the plot so the graph is contained
plot.zoomToFit();
// 10. Move key to top-left
plot.getPlotter()->setKeyPosition(JKQTPKeyInsideTopLeft);
// 11. show plotter and make it a decent size
plot.show();
plot.resize(800,800);
The result looks like this: